剖析0.1+0.2不等于0.3的原因

由errol发表于2025-10-03 | 分类为编程 | 标签为js、二进制

相信每一位js coder都曾看到或遇到过类似于0.1+0.2不等于0.3的问题，对于早已习惯了十进制的人来说，是非常违反常识的存在，可能还为此感到过困惑和不解。

图1 0.1+0.2 != 0.3

这其实一个关于二进制的问题，以前倒是写过一篇相关的文章，但现在已经忘得差不多了... 故起笔这篇文章，当做一次知识点复习。

主要的原因是，有一些浮点数，无法使用二进制精确地表示，如0.1，其底层二进制表示为0.0001100110011…，此时会导致精度丢失，本质上与十进制中无法精确表示一些分数一样，如1/3。

一般情况下，编程语言默认都遵循IEEE 754二进制浮点数算术标准，所以即使是c类、java、python、go等，也都存在相同的问题，而并非js独有。

顺便一提，即使转为整数计算，如(100+200)/1000，实际上也没解决问题。

虽然运行该表达式时，结果确实是0.3，也等于0.3，但其实是js"美化"了的结果，js引擎觉得你想要的应该是十进制里的0.3(有限小数)，而不是二进制的0.3(无限小数)，于是帮你抹去零头，并取一个近似的值。

图1 (100+200)/1000 = 0.3?

# 0.3也无法使用二进制精确表示: 

0.01001100110011001100110011001100110011001100110011001100110011...

可以通过以下方式查看精度更高的值：

与0.3相差无几，但不等于0.3。

图3 并非0.3

有且仅有1是浮点数的精确倍数时，才是准确的，如：

(0.25 + 0.5) === 0.75 // true

因为0.25和0.5都可以使用二进制精确地表示，分别是：0.01和0.1，不会出现精度丢失的问题。

以js为例，浮点数使用8字节64位表示，其基本的结构为：符号位(1) + 指数(11) + 有效数字(52)。

其中，指数是无符号整数，因此需要使用偏移量来表示负数，且IEEE 754有两个特殊指数值，0和2047，前者表示0或非规格化数，后者表示Infinity或NaN，所以实际上可用的只有1-2046。

为了保持对称(相对对称，保持以0为基准，往前是负数，往后是正数)，也就调出2023这个合适的偏移量。

最小：1 - 1023 = -1022

最小正正规数：≈ 2⁻¹⁰²² ≈ 2.2 × 10⁻³⁰⁸

最大：2046 - 1023 = +1023

最大数：≈ 2¹⁰²³ ≈ 8.9 × 10³⁰⁷

以0.1为例，转为一个二进制形式：

0.000110011001100110011001100110011001100110011001100110011001100110011001100110011001100110011

使用科学计数法表示为：

1.10011001100110011001100110011001100110011001100110011001100110011001100110011001100110011 x 2 ^ -4

然后截取小数点后52位作为存储的尾数，第53位用于决定是否进位，而由于第53位是1，因此需要对第52位进位，最终就是：

1.1001100110011001100110011001100110011001100110011010 x 2 ^ -4

注意，在存储时，因为前导1是固定不变的，所以无需存储，而只记录小数部分

所以，0.1的符号位是0(正数)，指数为-4 + 1023，尾数是1001100110011001100110011001100110011001100110011010。

以此类推，0.2为：

1.1001100110011001100110011001100110011001100110011010 x 2 ^ -3

符号位为0，指数为-3 + 1023，尾数为：1001100110011001100110011001100110011001100110011010。

将二者进行相加，也就是运行0.1 + 0.2的算术表达式：

对齐指数后操作。

  0.1100110011001100110011001100110011001100110011001101   × 2 ^ -3 
+ 1.1001100110011001100110011001100110011001100110011010   × 2 ^ -3  
-------------------------------------------------------------------
= 10.0110011001100110011001100110011001100110011001100111  × 2 ^ -3
= 1.00110011001100110011001100110011001100110011001100111  × 2 ^ -2

在将其转为十进制：

# 可以转为小数后，使用按权展开法。

0.0100110011001100110011001100110011001100110011001100111

0 + 0 + 2^-2 + 0 + 0 + 2^-5 + 2^-6 + 0 + 0 + 2^-9 + 2^-10...

当然，这样手动计算也未免太繁琐，还容易出错，因此可根据该思路设计算法：

function binaryStringToDecimal(binaryStr) {
    // 分割整数部分和小数部分
    const parts = binaryStr.split('.');
    const integerPart = parts[0];
    const fractionalPart = parts[1] || '';

    let decimal = 0;

    // 1. 转换整数部分
    if (integerPart !== '0' && integerPart !== '') {
        decimal += parseInt(integerPart, 2);
    }
    // 2. 转换小数部分
    for (let i=0; i<fractionalPart.length; i++) {
        if (fractionalPart[i] === '1') {
            decimal += Math.pow(2, -(i + 1));  // 2⁻¹, 2⁻², 2⁻³, ...
        }
    }
    return decimal;
}

调用方法：

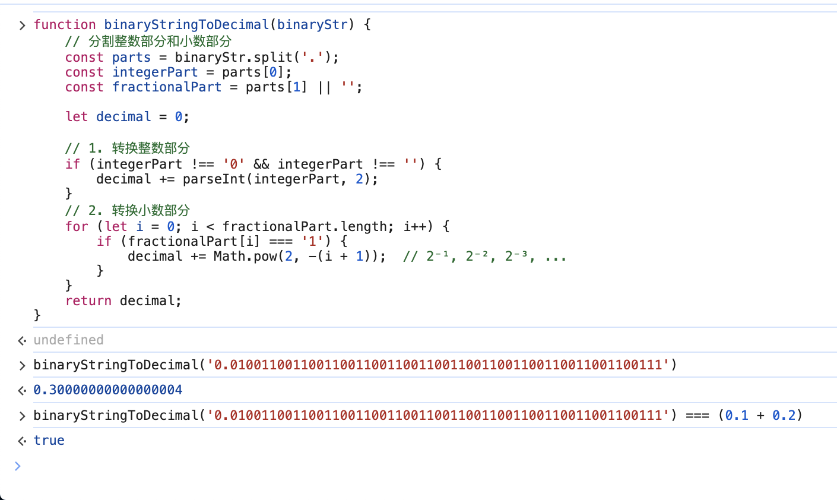
图4 方法调用结果

计算得出精确的0.30000000000000004，与0.1 + 0.2算术表达式的结果相等。

以上便是0.1+0.2不等于0.3问题的猫咪。

在实际项目中，如果有必要的话，可以使用精确数值类型，Decimal，可以达到精确的需求。

const Decimal = require('decimal.js');
let a = new Decimal(0.1);
let b = new Decimal(0.2);
let sum = a.plus(b);

console.log(sum.equals(0.3)); // true

大致上，内部使用整数来表示小数，避免小数运算。初始化时，将小数解析为整数部分和指数部分，如0.1，整数为1，指数为-1，使用科学计数法表示为：1 * 10 ^ -1；在输出时，则根据指数来定位小数点，如-1时，就在在整数前面，.1，即0.1。

当然，事实上，除非与金融行业相关，否则一般不会要求绝对精确；虽然不精确，但也是一个相当接近的值，所以可以采用截取小数的暴力方式。

相关文章